Codeforces Round 1037 Problem F "1-1-1, Free Tree!"
Solution for coding problem "1-1-1, Free Tree!"
Link: https://codeforces.com/contest/2126/problem/F
Time limit per test: 4 second
Memory limit per test: 256 megabytes
Problem description
Given a tree∗ with n vertices numbered from 1 to n. Each vertex has an initial color ai.
Each edge of the tree is defined by three numbers: ui, vi, and ci, where ui and vi are the endpoints of the edge, and ci is the edge parameter. The cost of the edge is defined as follows: if the colors of vertices ui and vi are the same, the cost is 0; otherwise, the cost is ci.
You are also given q queries. Each query has the form: repaint vertex v to color x. The queries depend on each other (after each query, the color change is preserved). After each query, you need to output the sum of the costs of all edges in the tree.
∗A tree is a connected graph without cycles.
Input
The first line contains an integer t (1 ≤ t ≤ 104) — the number of test cases.
The first line of each test case contains two integers n and q (1 ≤ n,q ≤ 2 ⋅ 105) — the number of vertices and the number of queries, respectively.
The second line contains n integers a1,a2,…,an (1 ≤ ai ≤ n), where the i-th number specifies the initial color of vertex i.
The next n−1 lines describe the edges of the tree. Each line contains three integers u, v, and c, denoting an edge between vertices u and v with parameter c (1 ≤ u,v ≤ n, 1 ≤ c ≤ 109).
The following q lines contain the queries. Each query contains two integers v and x — repaint vertex v to color x (1 ≤ v,x ≤ n).
It is guaranteed that the sum of n and the sum of q across all test cases do not exceed 2 ⋅ 105.
Output
For each query, output a single integer on a separate line — the sum of the costs of all edges in the tree after applying the corresponding query.
Example:
Input:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
4
1 1
1
1 1
2 3
1 1
1 2 10
1 2
2 2
1 1
5 4
1 2 1 2 3
1 2 5
2 3 3
2 4 4
4 5 7
3 2
5 2
1 2
2 3
4 3
1 1 2 2
1 2 2
2 3 6
2 4 8
3 1
4 1
2 2
Output:
1
2
3
4
5
6
7
8
9
10
11
0
10
0
10
12
5
0
12
8
0
16
Note
First test: n = 1, one vertex — no edges. Query: repaint a1 to 1, the sum of costs is 0.
Second test: n = 2, edge 1 − 2 (c = 10). Queries:
- a1 = 2: colors [2,1], cost is 10;
- a2 = 2: colors [2,2], cost 0;
- a1 = 1: colors [1,2], cost 10.
Third test: n = 5, edges: 1 − 2 (c = 5), 2 − 3 (c = 3), 2 − 4 (c = 4), 4 − 5 (c = 7). Initial colors [1,2,1,2,3]. Queries:
a3 = 2 → [1,2,2,2,3]: edges 1 − 2 (c = 5) and 4 − 5 (c = 7) give 12;
a5 = 2 → [1,2,2,2,2]: edge 1 − 2 (c = 5), cost 5;
a1 = 2 → [2,2,2,2,2]: cost is 0;
a2 = 3 → [2,3,2,2,2]: edges 1 − 2 (5), 2 − 3 (3), 2 − 4 (4) give 12.
Approach
My solution might be very complicated for beginners and uses quite some advanced algorithms and data structures (also specific to C++).
Unlike other problem, this solution will be more of a “it just works, it isn’t really a solution that can be explained well.” What I thought was that the only thing you need to care about the most is the parent.
For each node, we need to first precompute the parent of that node (except for the root, node 1) and the sum of the weights from a child to the node for every color that exists in their children. We can use Depth First Search (DFS) to figure both of them out. If you don’t know what DFS is, you can watch this YouTube Video by WilliamFiset or read this GeeksbyGeeks blog.
However, if we store all different colors for each node, we would use up about O(N^2) memory, which would exceed our memory limit (as N can be as large as 2 ⋅ 105). Instead, we can store a multiset (you can read this blog about what multisets are and their properties) for each node and only add the colors for each node that appear in their children. This would only have a memory of maximum O(N-1+Q) (N-1 edges with possibly Q changes and additions), which should be enough to fit our memory limit.
During this process, we will also figure out the current sum of edges without any changes done.
Now that we have precomputed everything we need, for each query, we will do two things. First, we need to check on our children. We need to add the weights of edges where the node (the one where we will change its color) and its children HAD the same color (before the change). Afterward, we have to delete the weights of edges where the node and its children HAVE the same color (after the change). This can be done in O(logN) for both operations because of the lower_bound function. It uses Binary Search to find the number (or position) where the value is bigger than or equal to a specified value. You can learn Binary Search from my blog post.
Afterward, we need to check with the node’s parent. This is why this solution works for this problem. If in the future the parent changes color, all information about the colors in the parent’s multiset would have been updated in the past changes. So, we can make the necessary changes. We can edit the multiset so that the sums are edited to the correct sums for each color and add/subtract from the current sum depending on the colors of each node (original and new).
This solution is very complicated an quite difficult to explain, so if you have any questions, please leave a comment.
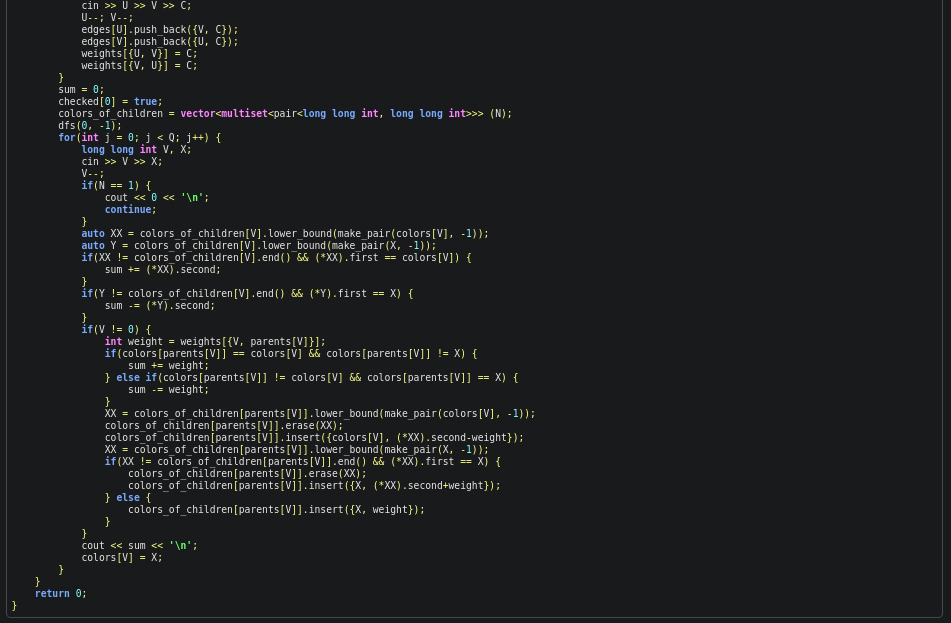
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include <iostream>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
using namespace std;
vector<long long int> parents;
vector<long long int> colors;
vector<long long int> checked;
vector<vector<pair<long long int, long long int>>> edges;
vector<multiset<pair<long long int, long long int>>> colors_of_children;
long long int sum;
map<pair<long long int, long long int>, long long int> weights;
void dfs(int node, int last_node) {
if(last_node != -1) {
if(colors_of_children[last_node].size() == 0) {
colors_of_children[last_node].insert({colors[node], weights[{last_node, node}]});
} else {
auto X = colors_of_children[last_node].lower_bound(make_pair(colors[node], (int)-1));
if(X == colors_of_children[last_node].end() || (*X).first != colors[node]) {
colors_of_children[last_node].insert({colors[node], weights[{last_node, node}]});
} else {
colors_of_children[last_node].erase(X);
colors_of_children[last_node].insert({colors[node], (*X).second+weights[{last_node, node}]});
}
}
}
for(int i = 0; i < edges[node].size(); i++) {
if(!checked[edges[node][i].first]) {
checked[edges[node][i].first] = true;
parents[edges[node][i].first] = node;
if(colors[edges[node][i].first] != colors[node]) sum += edges[node][i].second;
dfs(edges[node][i].first, node);
}
}
}
int main() {
int T;
cin >> T;
for(int i = 0; i < T; i++) {
int N, Q;
cin >> N >> Q;
colors = vector<long long int>(N);
for(int j = 0; j < N; j++) {
cin >> colors[j];
}
checked = vector<long long int>(N);
parents = vector<long long int>(N);
edges = vector<vector<pair<long long int, long long int>>>(N);
weights.clear();
for(int j = 0; j < N-1; j++) {
long long int U, V, C;
cin >> U >> V >> C;
U--; V--;
edges[U].push_back({V, C});
edges[V].push_back({U, C});
weights[{U, V}] = C;
weights[{V, U}] = C;
}
sum = 0;
checked[0] = true;
colors_of_children = vector<multiset<pair<long long int, long long int>>> (N);
dfs(0, -1);
for(int j = 0; j < Q; j++) {
long long int V, X;
cin >> V >> X;
V--;
if(N == 1) {
cout << 0 << '\n';
continue;
}
auto XX = colors_of_children[V].lower_bound(make_pair(colors[V], -1));
auto Y = colors_of_children[V].lower_bound(make_pair(X, -1));
if(XX != colors_of_children[V].end() && (*XX).first == colors[V]) {
sum += (*XX).second;
}
if(Y != colors_of_children[V].end() && (*Y).first == X) {
sum -= (*Y).second;
}
if(V != 0) {
int weight = weights[{V, parents[V]}];
if(colors[parents[V]] == colors[V] && colors[parents[V]] != X) {
sum += weight;
} else if(colors[parents[V]] != colors[V] && colors[parents[V]] == X) {
sum -= weight;
}
XX = colors_of_children[parents[V]].lower_bound(make_pair(colors[V], -1));
colors_of_children[parents[V]].erase(XX);
colors_of_children[parents[V]].insert({colors[V], (*XX).second-weight});
XX = colors_of_children[parents[V]].lower_bound(make_pair(X, -1));
if(XX != colors_of_children[parents[V]].end() && (*XX).first == X) {
colors_of_children[parents[V]].erase(XX);
colors_of_children[parents[V]].insert({X, (*XX).second+weight});
} else {
colors_of_children[parents[V]].insert({X, weight});
}
}
cout << sum << '\n';
colors[V] = X;
}
}
return 0;
}
Lines 1-6: imported all libraries needed and used the namespace std
Lines 7-13: initializes global variables and arrays
Lines 15-37: DFS function for precomputing all values and sums of edges for colors of children for each node (as shown in my approach)
Line 40-41: initializes T (test cases) and inputs them in
Line 42: starts a for loop for the number of test cases
Line 43-44: initializes and inputs in N and Q
Lines 45-48: initializes vector (array) and inputs in all colors of nodes
Lines 49-61: initializes vectors (arrays) and inputs in all edges with the two end nodes and the weights
Lines 62-65: starts the DFS explained above
Lines 66-102: calculates the answer after each query using the approach explained above
Then, the code continues this process from lines 43-102 for all other test cases.